Charge Displacement¶
The Charge-Displacement (CD) analysis is a simple method able of analyzing and quantifying the amount of charge transfer that occurs upon a bond formation between two interacting fragments. This tutorial shows three different examples how to calculate the Charge-Displacement function.
The CD function Δq(z) is defined as the partial integration along a chosen axis, z, of the electron density rearrangement Δρ(x,y,z’) taking place upon the bond formation:
It can be also used in combination with the NOCV theory (where the electron density rearrangement is defined with respect to the orthonormalized non-interacting fragments). More information about Natural Orbitals for Chemical Valence can be found at ETS-NOCV and in the EDA-NOCV tutorial. In this case the deformation density can be expressed as a sum of contributions (Δρk) defined by the NOCV pairs of complementary eigenfunctions (Ψ-k and Ψk) corresponding to eigenvalues -ν-k and νk with the same absolute value but opposite sign:
and the associated CD function (NOCV-CD) is simply defined as following:
This tutorial shows how to build the chemical integrands for evaluating the CD function in three different relevant examples:
Quantifying the CT contribution in closed-shell interacting fragments: case of noble metal-noble gas interaction in the Xe-AuF complex. [1]
Quantifying of the Dewar-Chatt-Duncanson bonding components (σ-donation and π-backdonation) in transition metal complex applying the CD function in combination of the NOCV theory (NOCV-CD). [2]
Application to open-shell systems to reveal competing pathways of proton-coupled electron transfer in oxidation catalysis (hydrogen-atom transfer, concerted proton-coupled electron transfer). [3]
In all cases the basic idea is to evaluate the different integrands (Δρ, Δρk or Δρα/β) using densf or directly from AMS-GUI which allow for their efficient mapping of a grid (CUBE format).
The CD function is evaluated numerically on the grid. This requires that you first download the PYCUBESCD suite of programs which is freely available (LGPL-3.0 License at GitHub).
Case 1: CT in closed-shell interacting fragments: Xe—AuF¶
The molecular structures needed for this tutorial are given here.
The molecular structures are properly aligned with the molecular axis along the z-axis. In general, one should optimize the structures first and align with the z-axis coinciding with the direction chosen for evaluating the CD function.
Note
The alignment is important. The z-axis defines the axis on which is performed the partial integration for evaluating the CD function. The fragments (Xe and AuF) have the geometry they possess within the complex.
1. Fragment Calculation¶
At first, a fragment calculation must be performed. The following steps from the Fragment Analysis tutorial can be followed. A script including the fragment calculation (step 1) and step 2 will be provided in step 2.
Xe-AuF structure. to add it as region
to add it as region
The .rkf file of the final fragment analysis (the adf.rkf in the XeAuF.results folder) is needed in the following step.
2. Generate CD function¶
The densf program must be used, which is an auxiliary program distributed with ADF suite. See the documentation of Densf: Volume Maps to generate a numerical representation of the electron densities associated with the XeAuF complex and the sum of the isolated Xe and AuF fragments. Herein, details for the definition of the grid can be found. We will map these quantities in the CUBE format. The only information necessary from the previous fragment calculation (Step 1) is the rkf file.
The following script can be used to generate a CUBE file using densf for the SCF electron density (Density SCF):
"$AMSBIN"/densf << eor
InputFile XeAuF.results/adf.rkf
Density SCF ! We require the SCF density to be mapped
CUBOutput XeAuF ! Output is the file: XeAuF%SCF%Density.cub
Grid
-10.0 -10.0 -10.0
100 100 100
1.0 0.0 0.0 15.03
0.0 1.0 0.0 15.03
0.0 0.0 1.0 15.03
End
eor
A CUBE file can also be generated using densf for the sum of the SCF electron densities of the isolated Xe and AuF fragments (Density SumFrag):
"$AMSBIN"/densf << eor
InputFile XeAuF.results/adf.rkf
CUBInput
Density SumFrag ! We require the Sum of SCF densities of the isolated Fragments
CUBOutput XeAuF ! Output is the file: XeAuF%SumFrag%Density.cub
Grid
-10.0 -10.0 -10.0
100 100 100
1.0 0.0 0.0 15.03
0.0 1.0 0.0 15.03
0.0 0.0 1.0 15.03
End
eor
Note
All densities must be mapped on the same numerical grid. This has been explicitly defined after the grid keyword in the densf input. This is important if you use the PYCUBESCD suite of programs to calculate the CD function in Step 3.
Now we use the PYCUBESCD suite of programs to make operations between Cube files and to generate the CD function. PYCUBESCD suite is freely available to download (LGPL-3.0 License at GitHub).
In the following command, $INSTALL is the directory where the PYCUBESCD program is installed. You make use of the pysub_cube.py file which is placed in the PY3 folder in the pycubescd-master.
Run the following command in order to generate the file diff_XeAuF.cub, which contains the numerical representation of the electron density difference between the XeAuF molecule (cube file: XeAuF%SCF%Density.cub) and the sum of the electron density of the Xe and AuF fragments (cube file: XeAuF%SumFrag%Density.cub) obtained in the Step 2:
export INSTALL=/path/to/pycubescd-master
amspython $INSTALL/PY3/pysub_cube.py -f1 XeAuF%SCF%Density.cub -f2 XeAuF%SumFrag%Density.cub -o diff_XeAuF.cub
This file (diff_XeAuF.cub) can be easily visualized within AMS-GUI:
 → View
→ View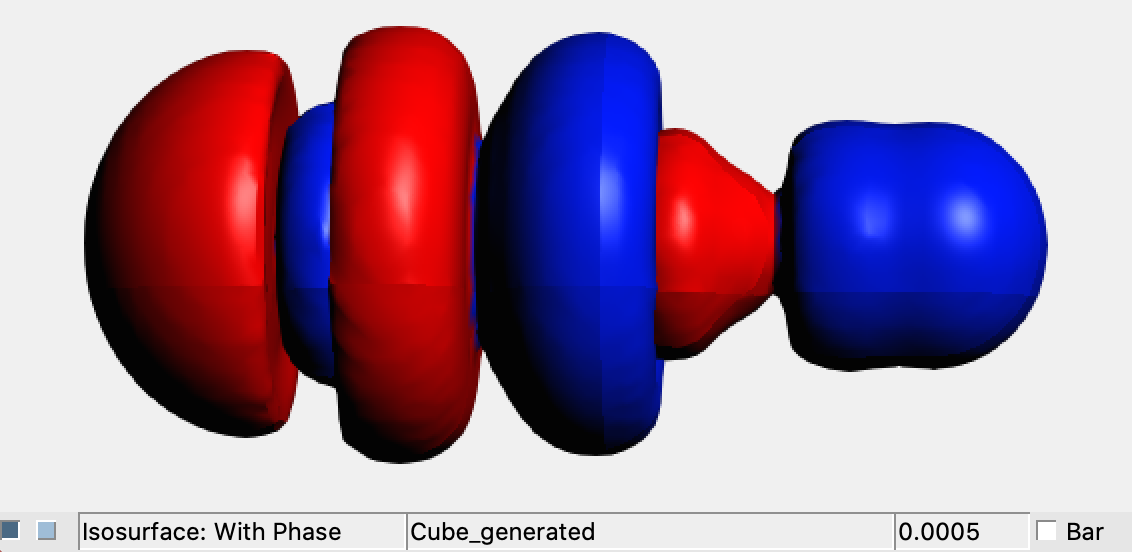
The CD function can be generated by using the pycd_simple.py program available in PYCUBESCD suite ($INSTALL is the directory where the PYCUBESCD program is installed):
amspython $INSTALL/PY3/pycd_simple.py -f diff_XeAuF.cub
The result is a text format file (diff_XeAuF.cub_cdz.txt) which contains the numerical representation of the CD function. It can be easily visualized with a 2D-plot software.
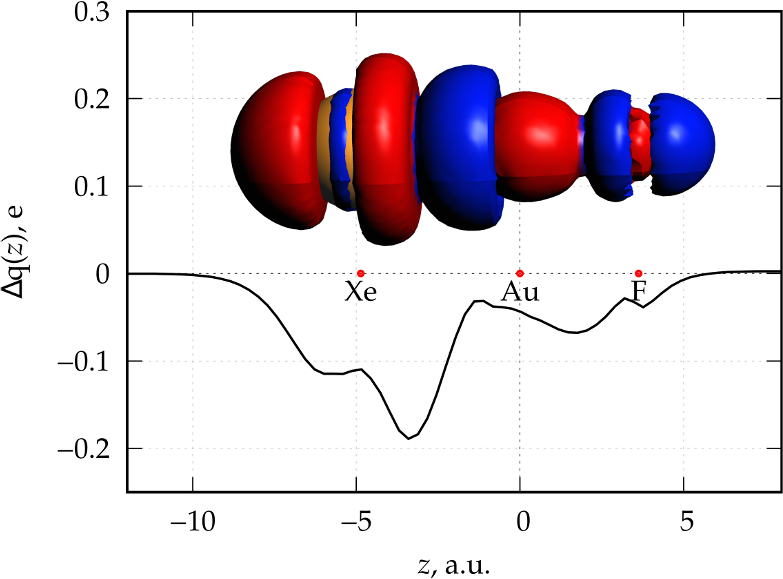
CD function via AMSview Line graph
 → View
→ View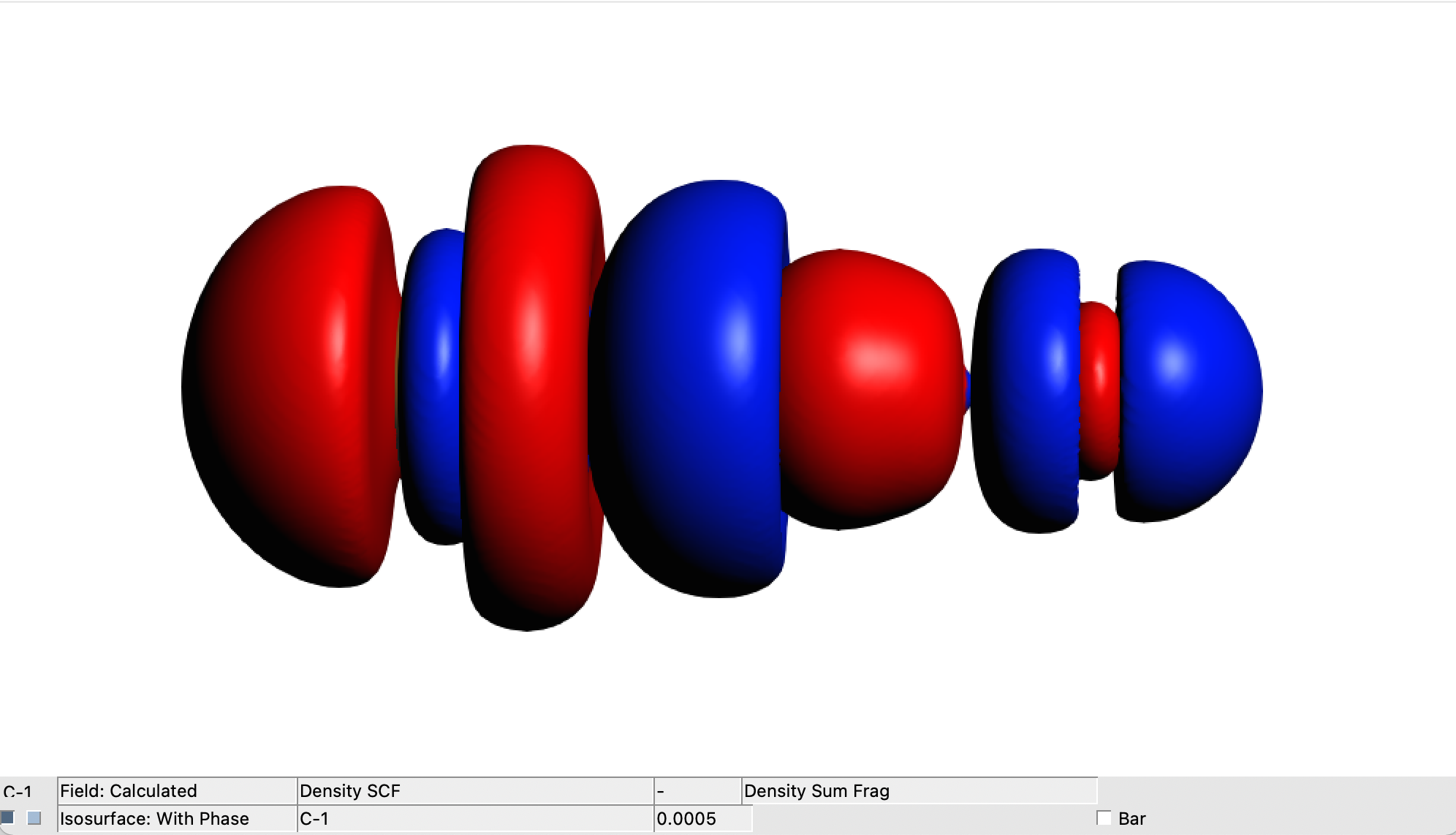
To get the CD function we need to define a line through the molecule. For each point along this line all values in a plane through point perpendicular to the line should be integrated. And finally the values along the line should be integrated. This functionality is part of the LineGraph in AMSview:
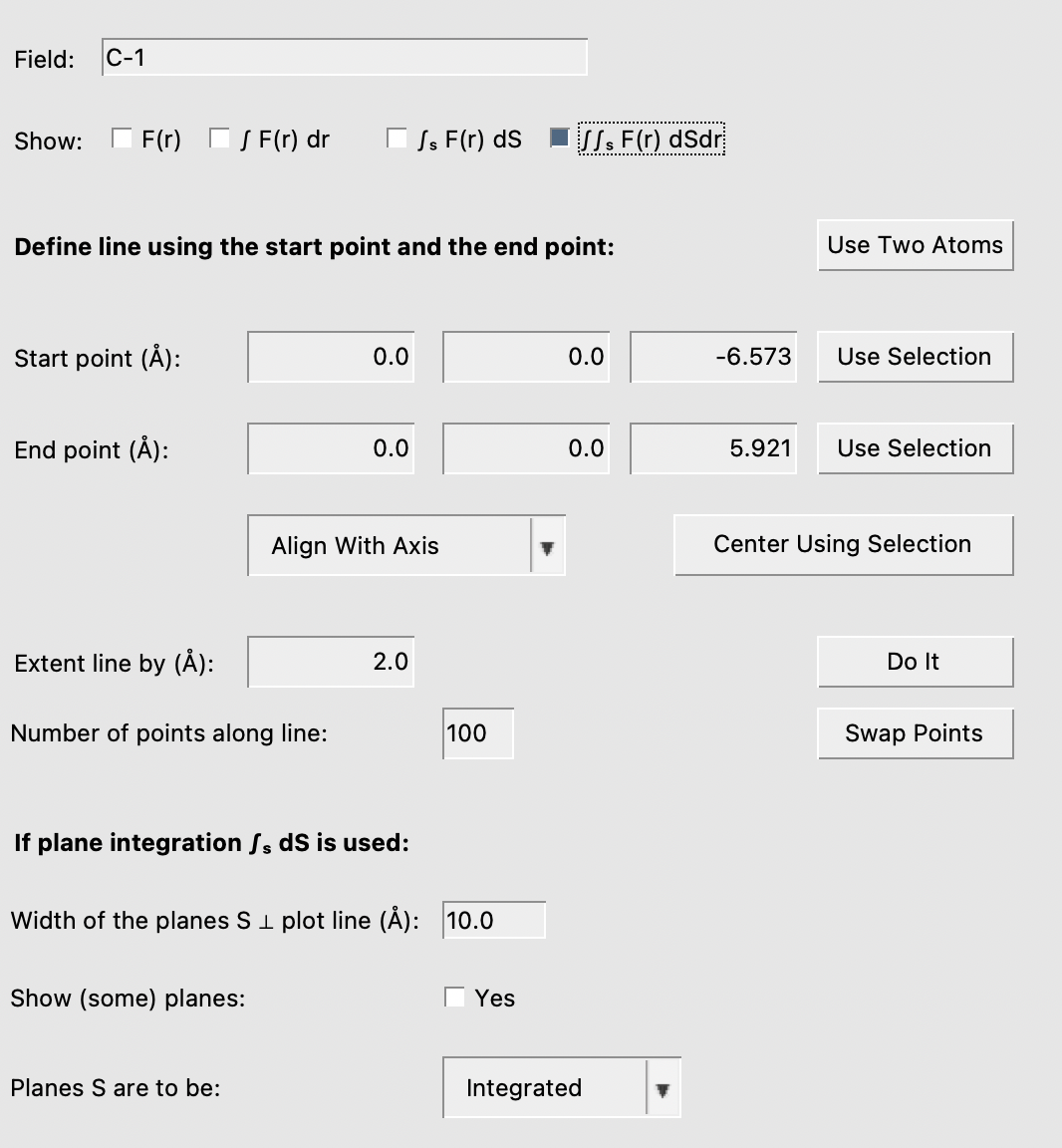
In the graph window you will see the result:
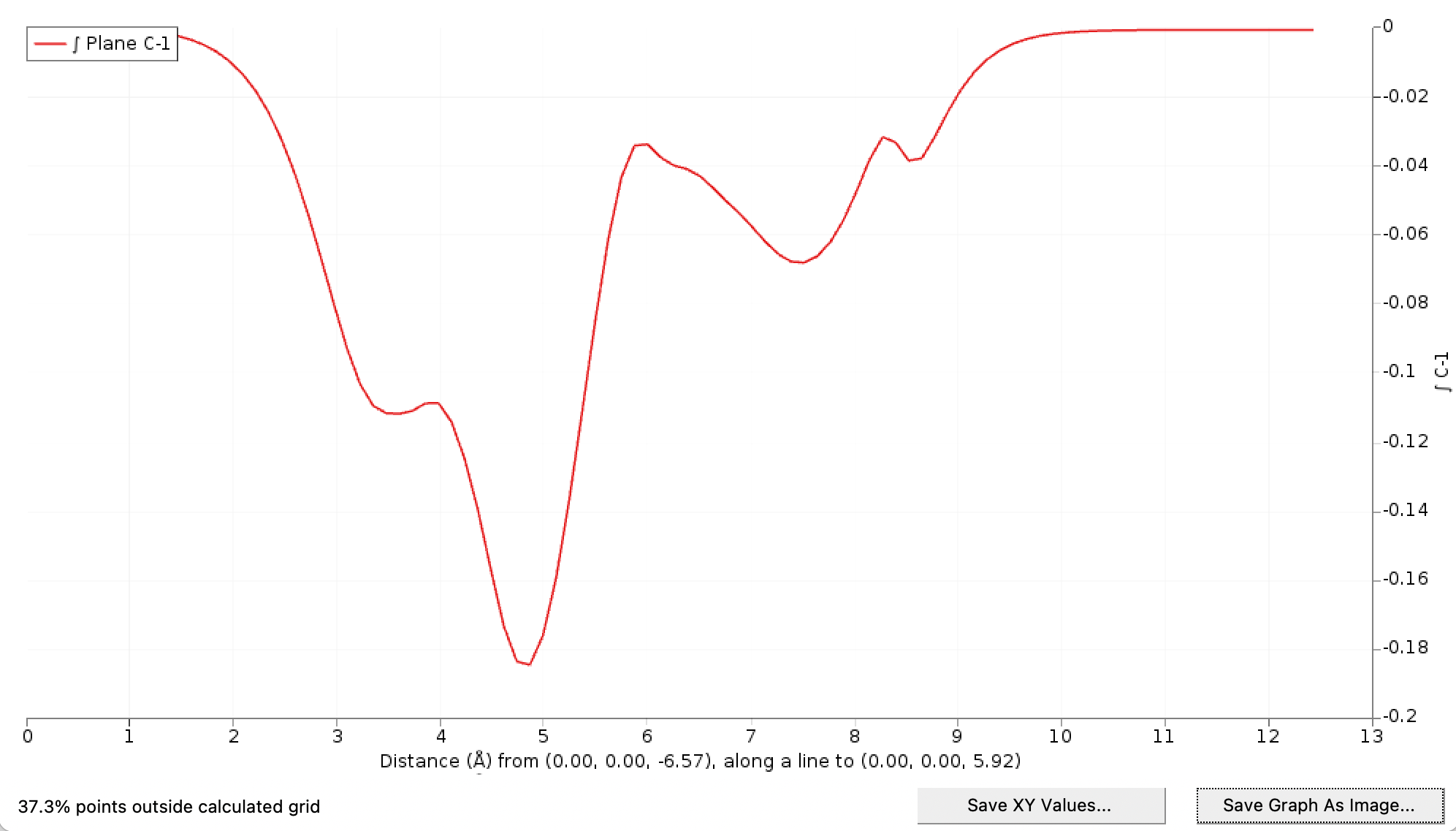
Note that the grid used is not large enough to provide data for all points sampled by the planes over which is integrated. You can see this in the lower left. To fix this, one can extent the grid:
This action has no effect on the graph, as the extra grid points have no significant contribution to the CD function.
In the details window there are more ways to control the line, which is not very relevant in this case. Another option is to show the integration planes, which visually gives you an idea of the size of the planes over which the grid is sampled to calculate the integrals over the planes.

You can adjust the size of the planes, and the number of points along the line and the planes using the controls in the Details window.
Case 2: Dewar-Chatt-Duncanson bonding components in a transition metal complex (NOCV-CD)¶
This tutorial shows how to generate the NOCV deformation densities (Δρk) and export them on a numerical grid (CUBE file format) directly using AMS-GUI. The associated CD functions (Δqk) are evaluated numerically using the PYCUBESCD suite of programs, freely available at GitHub.
The transition state complex needed for this tutorial is given here.
Note
The alignment of the molecule is important. The z-axis defines the axis on which is performed the partial integration for evaluating the CD function. In this case the integration axis is defined as the axis passing for the Ni atom and the midpoint of the CC triple bond of the coordinated alkyne.
1. Fragment Calculation¶
transition state complex to add it as region
to add it as region
2. Visualize NOCV deformation densities¶
The NOCV deformation densities can be visualized by performing the following steps:
 → View of the Fragment Calculation
→ View of the Fragment Calculation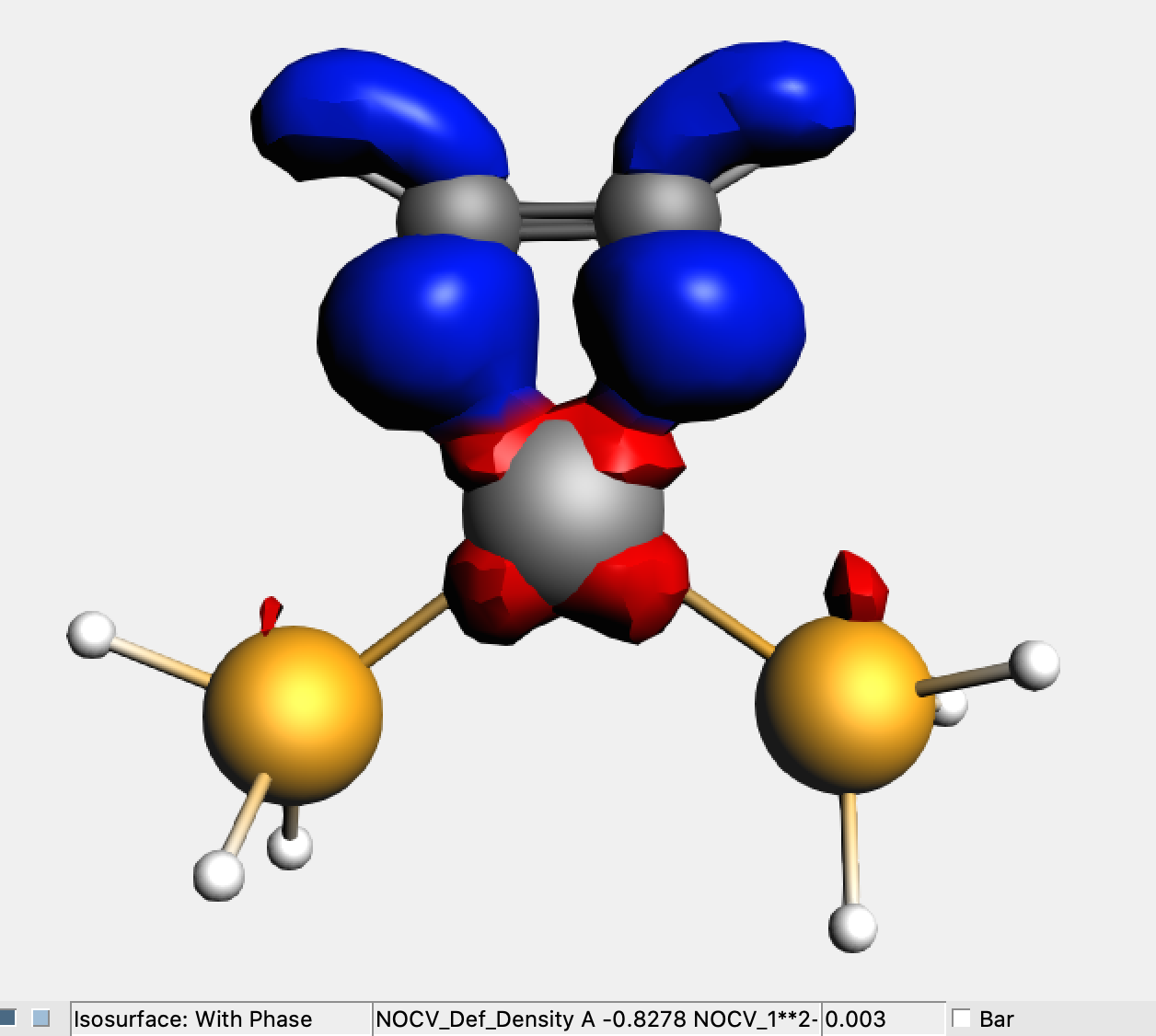
In the above figure is shown the deformation density (Δρ1) associated with the largest NOCV eigenvalue. It clearly represents the metal-to-substrate π-backdonation (red/blue colored isodensity surface defines electron density depletion/accumulation).
3. Generate a CUBE file¶
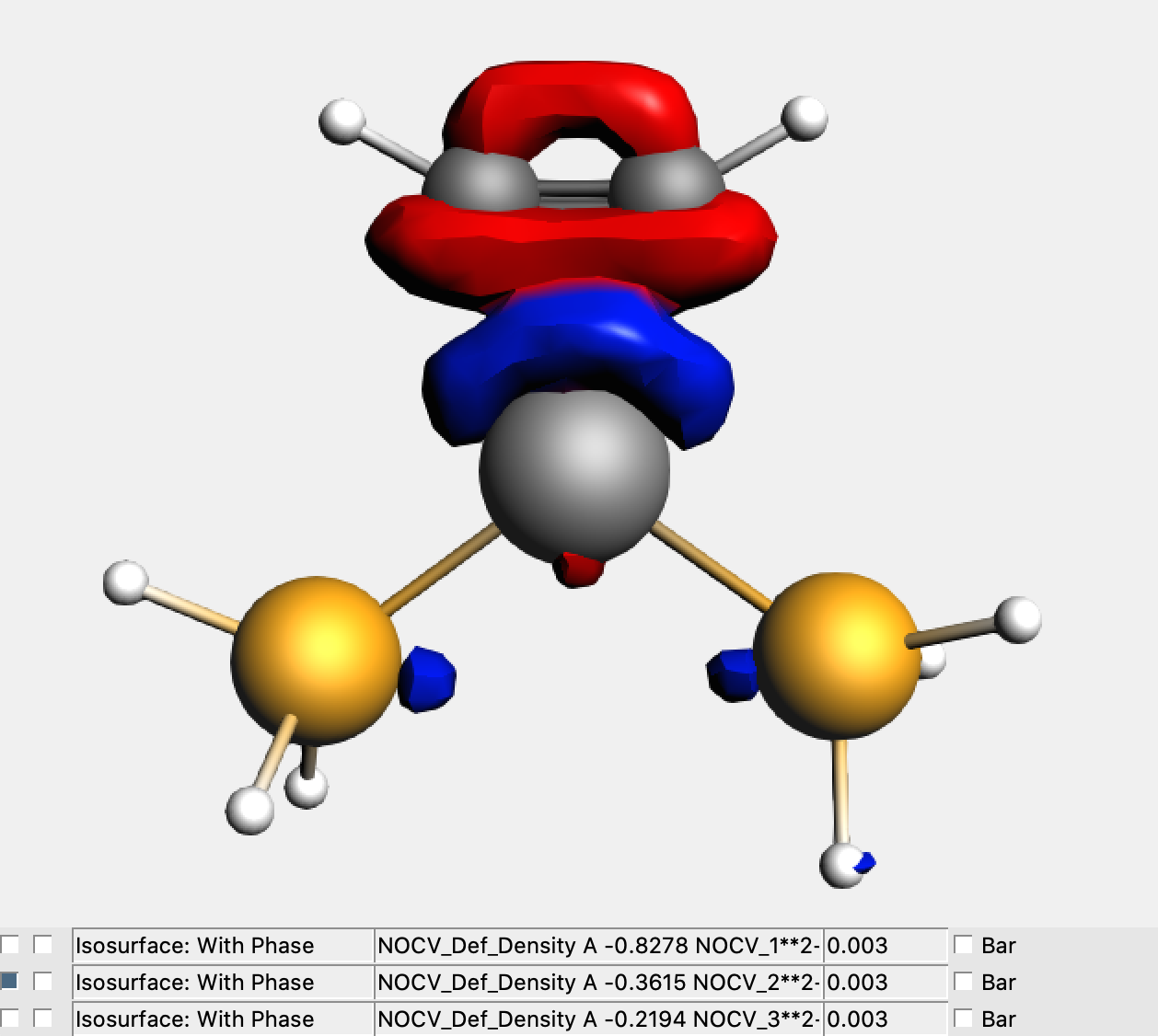
One starts with adding all the NOCV deformation densities you want to map in Cube File format. For instance, in the below example we chose those associated with the three largest eigenvalues, namely 0.8278, 0.3615 and 0.2194. The isodensity surface in the figure is related to Δρ2, which is clearly related to the σ-substrate-to-metal donation component. You add the NOCV deformation densities with:
The CUBE file can be generated now:
Note
Typically the Medium setting for the Grid is sufficient to obtain accurate CD functions. Clearly, the larger the grid is, the larger the size of the generated Cube files will be. For instance using Medium Grid the three Cube Files associated at Δρ1,Δρ2,Δρ3 have a size of 4.3MB (the latter increases to 34.3MB whether one sets Fine Grid to generate Cube Files).
4. CD functions for the NOCV deformation densities¶
The CD functions are generated using the pycd_simple.py program available in PYCUBESCD suite (exactly as done in the Case 1, step 3):
Give the following command line in the directory where the Cube Files associated at Δρ1, Δρ2, and Δρ3 have been generated (in the .results folder) and in which $INSTALL is the directory where the PYCUBESCD program is installed:
amspython $INSTALL/PY3/pycd_simple.py -f 215--Medium-0.cube%NOCV%SumDensities_A_1.cub
amspython $INSTALL/PY3/pycd_simple.py -f 218--Medium-0.cube%NOCV%SumDensities_A_2.cub
amspython $INSTALL/PY3/pycd_simple.py -f 221--Medium-0.cube%NOCV%SumDensities_A_3.cub
The results are three text format files (.cub_cdz.txt) which contains the numerical representation of the CD functions associated with Δρ1, Δρ2, and Δρ3. They can be easily visualized with a 2D-plot software. The picture below can be obtained combining the 3D isosurface pictures of the NOCV density deformations.

Case 3: Open-Shell CD in the HAT mechanism of the TauD-J intermediate¶
This tutorial shows how to generate the spin-density difference and the total-density difference (Δρα,Δρβ,Δρtot) and export them on a numerical grid (CUBE file format) using densf. The associated CD functions (Δqα,Δqβ,Δqtot) are then evaluated numerically using the PYCUBESCD suite of programs, freely available at GitHub.
1. Unrestricted Calculations¶
First, we need to perform a set of unrestricted ADF calculations on the transition state structure of the TauD-J__C2 H6 model system.
The TauD-J intermediate features a FeIV =O unit which is the H-abstracting species.
The two constituting fragments to consider are the Fe=O moiety of TauD-J and the C2 H6 substrate, in the position they occupy in the transition state geometry.
The molecular structures needed for this tutorial can be downloaded here.
Note
The alignment of the molecule is important. The z-axis defines the axis on which is performed the partial integration for evaluating the CD function. In this case the integration axis is defined as the axis through the Fe=O bond.
Three independent calculations will be performed: (i) TauD-J__C2 H6 model system (FeO_CH) (ii) TauD-J fragment (FeO) and (iii) ethane fragment.
TauD-J__C2H6 system4.0
Now, the other two single point calculations can be performed:
TauD-J fragment in a new AMSinputethane fragment in a new AMSinput0.0The adf.rkf files of these calculations are needed for the following step.
2. Generate CUBE files¶
We use densf to generate a numerical representation of the electron spin-densities associated with the unrestricted calculations performed on the (i) TauD-J__C2 H6 model system (FeO_CH) (ii) TauD-J fragment (FeO) and (iii) ethane fragment (CH).
We map these quantities in the CUBE format. The only information necessary from previous single point calculations are the adf.rkf files.
The following script can be used to generate the CUBE files for the α- and β-spin electron densities of FeO, CH and FeO_CH.
for job in "FeO" "CH" "FeO_CH"; do
$AMSBIN/densf << eor
InputFile $job.results/adf.rkf
Density SCF
CUBOutput $job
Grid
-10.0 -10.0 -10.0
300 300 350
1.0 0.0 0.0 20.0
0.0 1.0 0.0 20.0
0.0 0.0 1.0 20.0
End
eor
done
Note
As in any unrestricted calculation, we will get the α- and β-spin electron density as a result.
3. Obtain density differences¶
We now use the PYCUBESCD suite of programs to make operations between Cube files and to obtain the spin-density differences (Δρα, Δρβ) and the total density difference (Δρ). These density differences will be then integrated along the z-axis to retrieve the corresponding CD functions.
Use the command lines below in the directory where your just generated cube files are placed. The $INSTALL need to be changed to the directory where the PYCUBESCD program is installed, and when you have named the cuboutput differently (than FeO, CH and FeO_CH) change the names of the input cube files as well.
amspython $INSTALL/PY3/pyadd_cube.py -f1 FeO%SCF%Density_A.cub -f2 CH%SCF%Density_A.cub -o SumFrag_Density_A.cub
amspython $INSTALL/PY3/pyadd_cube.py -f1 FeO%SCF%Density_B.cub -f2 CH%SCF%Density_B.cub -o SumFrag_Density_B.cub
amspython $INSTALL/PY3/pysub_cube.py -f1 FeO_CH%SCF%Density_A.cub -f2 SumFrag_Density_A.cub -o diff_FeO_CH_A.cub
amspython $INSTALL/PY3/pysub_cube.py -f1 FeO_CH%SCF%Density_B.cub -f2 SumFrag_Density_B.cub -o diff_FeO_CH_B.cub
amspython $INSTALL/PY3/pyadd_cube.py -f1 diff_FeO_CH_A.cub -f2 diff_FeO_CH_B.cub -o diff_FeO_CH.cub
The generated diff_FeO_CH_A.cub, diff_FeO_CH_B.cub and diff_FeO_CH.cub files contain the numerical representation of the electron (spin) density difference between the FeO_CH system and the sum of the electron (spin) densities of the FeO and CH fragments.
These files can be easily visualized within AMS-GUI in the same manner as for Case1 and Case2:
 → View
→ View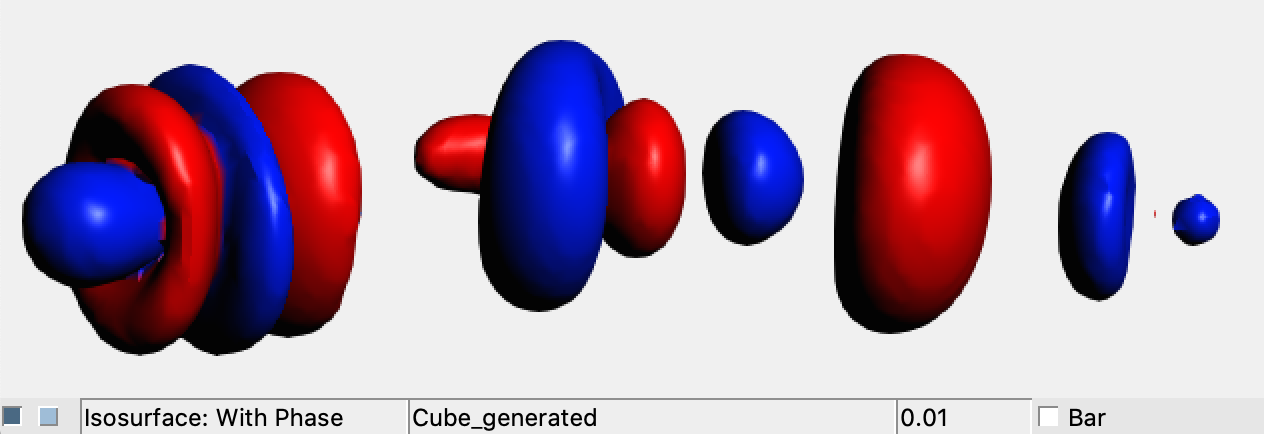
4: Generate the CD functions¶
The CD functions are finally generated using the pycd_simple.py program available in PYCUBESCD suite.
Again, the $INSTALL needs to be changed to the directory where the PYCUBESCD program is installed.
amspython $INSTALL/PY3/pycd_simple.py -f diff_FeO_CH_A.cub
amspython $INSTALL/PY3/pycd_simple.py -f diff_FeO_CH_B.cub
amspython $INSTALL/PY3/pycd_simple.py -f diff_FeO_CH.cub
This results in three text formal files ( .cub_cdz.txt) which contains the numerical representation of the CD functions associated with Δρα, Δρβ and Δρtot. They can be easily visualized with a 2D-plot software. The picture below can be obtained combining the isosurface picture of the total density difference and the three CD functions.
