Molecule¶

class Molecule(filename=None, inputformat=None, positions=None, numbers=None, lattice=None, **other)[source]¶

A class representing the molecule object.

An instance of this class has the following attributes:

• atoms – list of Atom objects that belong to the molecule

• bonds – list of Bond objects between atoms listed in atoms

• lattice – list of lattice vectors in case of periodic structures

• properties – Settings instance storing all other information about the molecule

Note

Each Atom in atoms list and each Bond in bonds list has a reference to the parent molecule. Moreover, each atom stores the list of bonds it’s a part of and each bond stores references to atoms it bonds. That creates a complex net of references between objects that are part of a molecule. Consistency of this data is crucial for proper functioning of many methods. Because of that it is advised not to modify contents of atoms and bonds by hand. When you need to alter your molecule, methods add_atom(), delete_atom(), add_bond() and delete_bond() can be used to ensure that all these references are updated properly.

Creating a Molecule object for your calculation can be done in several ways. You can start with an empty molecule and manually add all atoms (and bonds, if needed):

mol = Molecule()
mol.add_atom(Atom(atnum=1, coords=(0,0,0)))
mol.add_atom(Atom(atnum=1, coords=(d,0,0)))

This approach can be useful for building small molecules, but in general it’s not very practical. If coordinates and atom numbers are available, instantiation can be done by passing a value to the positions, numbers and optionally the lattice arguments:

xyz     = np.random.randn(10,3) # 10 atoms, 3 coordinates per atom
numbers = 10*[6] # 10 carbon atoms. If left None, will initialize to dummy atoms
lattice = [[1,2,3], [1,2,3]] # lattice should have a shape of {1,2,3}x3
mol     = Molecule(positions=xyz, numbers=numbers, lattice=lattice)

Alternatively, one can import atomic coordinates from some external file:

mol = Molecule('xyz/Benzene.xyz')

The constructor of a Molecule object accepts four arguments that can be used to supply this information from a file in your filesystem. filename should be a string with a path (absolute or relative) to such a file. inputformat describes the format of the file. Currently, the following formats are supported: xyz, mol, mol2 and pdb. If inputformat is ase the file reader engine of the ASE.io module is used, enabling you to read all input formats supported by ASE interface. See read() for further details. If the inputformat argument is not supplied, PLAMS will try to deduce it by examining the extension of the provided file, so in most of cases it is not needed to use inputformat, if only the file has the proper extension. Some formats (xyz and pdb) allow to store more than one geometry of a particular molecule within a single file. See the respective read() function for details how to access them. All other keyword arguments will be passed to the appropriate read function for the selected or determined file format.

If a Molecule is initialized from an external file, the path to this file (filename argument) is stored in properties.source. The base name of the file (filename without the extension) is kept in properties.name.

It is also possible to write a molecule to a file in one of the formats mentioned above or using the ASE.io engine. See write() for details.

The lattice attribute is used to store information about lattice vectors in case of periodic structures. Some job types will automatically use that data while constructing input files. lattice should be a list of up to 3 vectors (for different types of periodicity: chain, slab or bulk), each of which needs to be a list or a tuple of 3 numbers.

Lattice vectors can be directly read from and written to xyz files using the following convention (please mind the fact that this is an unofficial extension to the XYZ format):

3

    H      0.000000      0.765440     -0.008360
    O      0.000000      0.000000      0.593720
    H      0.000000     -0.765440     -0.008360
VEC1       3.000000      0.000000      0.000000
VEC2       0.000000      3.000000      0.000000
VEC3       0.000000      0.000000      3.000000

For 1D (2D) periodicity please supply only VEC1 (VEC1 and VEC2). Writing lattice vectors to xyz files can be disabled by simply resetting the lattice attribute:

mol.lattice = []

The detailed description of all available methods is presented below. Many of these methods require arguments that are atoms belonging to the current molecule. It can by done by using a reference to an Atom object present it the atoms list, but not by passing a number of an atom (its position within atoms list). Unlike some other tools, PLAMS does not use integer numbers as primary identifiers of atoms. It is done to prevent problems when atoms within a molecule are reordered or some atoms are deleted. References to Atom or Bond objects can be obtained directly from atoms or bonds lists, or with dictionary-like bracket notation:

>>> mol = Molecule('xyz/Ammonia.xyz')
>>> mol.guess_bonds()
>>> print(mol)
  Atoms:
    1         H      0.942179      0.000000     -0.017370
    2         H     -0.471089      0.815951     -0.017370
    3         N      0.000000      0.000000      0.383210
    4         H     -0.471089     -0.815951     -0.017370
  Bonds:
   (1)--1.0--(3)
   (2)--1.0--(3)
   (3)--1.0--(4)
>>> at = mol[1]
>>> print(at)
         H      0.942179      0.000000     -0.017370
>>> b = mol[(1,3)]
>>> print(b)
(         H      0.942179      0.000000     -0.017370 )--1.0--(         N      0.000000      0.000000      0.383210 )
>>> b = mol[(1,4)]
>>> print(b)
None

Note

For the purpose of mol[i] notation, the numbering of atoms within a molecule starts with 1. Negative integers can be used to access atoms enumerated in the reversed order (mol[-1] for the last atom etc.)

However, if you feel more familiar with identifying atoms by natural numbers, you can use set_atoms_id() to equip each atom of the molecule with id attribute equal to atom’s position within atoms list. This method can also be helpful to track changes in your molecule during tasks that can reorder atoms.

__init__(filename=None, inputformat=None, positions=None, numbers=None, lattice=None, **other)[source]¶

copy(atoms=None)[source]¶

Return a copy of the molecule. The copy has atoms, bonds and all other components distinct from the original molecule (it is so called “deep copy”).

By default the entire molecule is copied. It is also possible to copy only some part of the molecule, indicated by atoms argument. It should be a list of atoms that belong to the molecule. If used, only these atoms, together with any bonds between them, are copied and included in the returned molecule.

add_molecule(other, copy=False, margin=-1)[source]¶

Add some other molecule to this one:

protein += water

If copy is True, other molecule is copied and the copy is added to this molecule. Otherwise, other molecule is directly merged with this one The properties of this molecule are soft_updated with the properties of the other molecules.

margin: float

If <0, keep the coordinates of other. If >=0, all atoms in the other molecule will have at least this distance (in angstrom) to all atoms in self.

_validate_atom(atom, is_new=False, msg='')[source]¶

Validate whether an Atom instance either belongs to this molecule, or is new. If validation fails, a MoleculeError is raised.

Parameters:

• atom – atom to validate

• is_new – whether atom is new and should not be part of this molecule

• msg – error message to include at the start of any raised error

_validate_bond(bond, is_new=False, validate_atoms=True, msg='')[source]¶

Validate whether an Bond instance either belongs to this molecule, or is new. If validation fails, a MoleculeError is raised.

Parameters:

• bond – bond to validate

• is_new – whether bond is new and should not be part of this molecule

• msg – error message to include at the start of any raised error

add_atom(atom, adjacent=None)[source]¶

Add a new atom to the molecule.

atom should be an Atom instance that does not belong to any molecule. Bonds between the new atom and other atoms of the molecule can be automatically added based on adjacent argument. It should be a list describing atoms of the molecule that the new atom is connected to. Each element of adjacent list can either be a pair (Atom, order) to indicate new bond’s order (use Bond.AR for aromatic bonds) or an Atom instance (a single bond is created in this case).

Example:

mol = Molecule() #create an empty molecule
h1 = Atom(symbol='H', coords=(1.0, 0.0, 0.0))
h2 = Atom(symbol='H', coords=(-1.0, 0.0, 0.0))
o = Atom(symbol='O', coords=(0.0, 1.0, 0.0))
mol.add_atom(h1)
mol.add_atom(h2)
mol.add_atom(o)
mol.add_atom(Atom(symbol='C', coords=(0.0, 0.0, 0.0)), adjacent=[h1, h2, (o,2)])

delete_atom(atom)[source]¶

Delete an atom from the molecule.

atom should be an Atom instance that belongs to the molecule. All bonds containing this atom are removed too.

Examples:

#delete all hydrogens
mol = Molecule('protein.pdb')
hydrogens = [atom for atom in mol if atom.atnum == 1]
for i in hydrogens: mol.delete_atom(i)

#delete first two atoms
mol = Molecule('geom.xyz')
mol.delete_atom(mol[1])
mol.delete_atom(mol[1]) #since the second atom of original molecule is now the first

add_bond(arg1, arg2=None, order=1)[source]¶

Add a new bond to the molecule.

This method can be used in two different ways. You can call it with just one argument being a Bond instance (other arguments are then ignored):

>>> b = Bond(mol[2], mol[4], order=Bond.AR) #create aromatic bond between 2nd and 4th atom
>>> mol.add_bond(b)

The other way is to pass two atoms (and possibly bond order) and new Bond object will be created automatically:

>>> mol.add_bond(mol[2], mol[4], order=Bond.AR)

In both cases both atoms that are bonded have to belong to the molecule, otherwise an exception is raised.

delete_bond(arg1, arg2=None)[source]¶

Delete a bond from the molecule.

Just like add_bond(), this method accepts either a single argument that is a Bond instance, or two arguments being instances of Atom. In both cases objects used as arguments have to belong to the molecule.

delete_all_bonds()[source]¶

Delete all bonds from the molecule.

find_bond(atom1, atom2)[source]¶

Find and return a bond between atom1 and atom2. Both atoms have to belong to the molecule. If no bond between chosen atoms exists, the returned value is None.

set_atoms_id(start=1)[source]¶

Equip each atom of the molecule with the id attribute equal to its position within atoms list.

The starting value of the numbering can be set with start (starts at 1 by default).

unset_atoms_id()[source]¶

Delete id attributes of all atoms.

neighbors(atom)[source]¶

Return a list of neighbors of atom within the molecule.

atom has to belong to the molecule. Returned list follows the same order as the bonds attribute of atom.

bond_matrix()[source]¶

Return a square numpy array with bond orders. The size of the array is equal to the number of atoms.

separate()[source]¶

Separate the molecule into connected components.

Returned is a list of new Molecule objects (all atoms and bonds are disjoint with the original molecule). Each element of this list is identical to one connected component of the base molecule. A connected component is a subset of atoms such that there exists a path (along one or more bonds) between any two atoms. Usually these connected components are molecules.

Example:

>>> mol = Molecule('xyz_dimers/NH3-H2O.xyz')
>>> mol.guess_bonds()
>>> print(mol)
  Atoms:
    1         N     -1.395591     -0.021564      0.000037
    2         H     -1.629811      0.961096     -0.106224
    3         H     -1.862767     -0.512544     -0.755974
    4         H     -1.833547     -0.330770      0.862307
    5         O      1.568501      0.105892      0.000005
    6         H      0.606736     -0.033962     -0.000628
    7         H      1.940519     -0.780005      0.000222
  Bonds:
   (5)--1.0--(7)
   (5)--1.0--(6)
   (1)--1.0--(3)
   (1)--1.0--(4)
   (1)--1.0--(2)
>>> x = mol.separate()
>>> for i in x: print(i)
  Atoms:
    1         N     -1.395591     -0.021564      0.000037
    2         H     -1.629811      0.961096     -0.106224
    3         H     -1.862767     -0.512544     -0.755974
    4         H     -1.833547     -0.330770      0.862307
  Bonds:
   (1)--1.0--(3)
   (1)--1.0--(4)
   (1)--1.0--(2)

  Atoms:
    1         O      1.568501      0.105892      0.000005
    2         H      0.606736     -0.033962     -0.000628
    3         H      1.940519     -0.780005      0.000222
  Bonds:
   (1)--1.0--(3)
   (1)--1.0--(2)

guess_bonds(atom_subset=None, dmax=1.28, metal_atoms=True)[source]¶

Try to guess bonds in the molecule based on types and positions of atoms.

All previously existing bonds are removed. New bonds are generated based on interatomic distances and information about maximal number of bonds for each atom type (connectors property, taken from PeriodicTable).

The problem of finding molecular bonds for a given set of atoms in space does not have a general solution, especially considering the fact the chemical bond in itself is not a precisely defined concept. For every method, no matter how sophisticated, there will always be corner cases for which the method produces disputable results. Moreover, depending on the context (area of application) the desired solution for a particular geometry may vary. Please do not treat this method as an oracle always providing a proper solution. The algorithm used here gives very good results for geometries that are not very far from the optimal geometry, especially consisting of lighter atoms. All kinds of organic molecules, including aromatic ones, usually work very well. Problematic results can emerge for transition metal complexes, transition states, incomplete molecules etc.

The algorithm used scales as n log n where n is the number of atoms.

The atom_subset argument can be used to limit the bond guessing to a subset of atoms, it should be an iterable container with atoms belonging to this molecule.

The dmax argument gives the maximum value for ratio of the bond length to the sum of atomic radii for the two atoms in the bond.

metal_atomsbool

If True, bonds to metal atoms will be guessed. They are often useful for visualization. The bond order for any bond to a metal atom will be set to 1.

Warning

This method works reliably only for geometries representing complete molecules. If some atoms are missing (for example, a protein without hydrogens) the resulting set of bonds would usually contain more bonds or bonds with higher order than expected.

guess_system_charge()[source]¶

Attempt to guess the charge of the full system based on connectivity

guess_atomic_charges(adjust_to_systemcharge=True, keep_hydrogen_charged=False, depth=1, electronegativities=None)[source]¶

Return a list of guessed charges, one for each atom, based on connectivity

• depth – The electronegativity of an atom is determined all its neighbors up to depth

• electronegativities – A dictionary containing electronegativity values for the electronegative elements

Note: Fairly basic implementation that will not always yield reliable results

in_ring(arg)[source]¶

Check if an atom or a bond belonging to this Molecule forms a ring. arg should be an instance of Atom or Bond belonging to this Molecule.

supercell(*args)[source]¶

Return a new Molecule instance representing a supercell build by replicating this Molecule along its lattice vectors.

One should provide in input an integer matrix \(T_{i,j}\) representing the supercell transformation (\(\vec{a}_i' = \sum_j T_{i,j}\vec{a}_j\)). The size of the matrix should match the number of lattice vectors, i.e. 3x3 for 3D periodic systems, 2x2 for 2D periodic systems and one number for 1D periodic systems. The matrix can be provided in input as either a nested list or as a numpy matrix.

For a diagonal supercell expansion (i.e. \(T_{i \neq j}=0\)) one can provide in input n positive integers instead of a matrix, where n is number of lattice vectors in the molecule. e.g. This mol.supercell([[2,0],[0,2]]) is equivalent to mol.supercell(2,2).

The returned Molecule is fully distinct from the current one, in a sense that it contains a different set of Atom and Bond instances. However, each atom of the returned Molecule carries an additional information about its origin within the supercell. If atom is an Atom instance in the supercell, atom.properties.supercell.origin points to the Atom instance of the original molecule that was copied to create atom, while atom.properties.supercell.index stores the tuple (with length equal to the number of lattice vectors) with cell index. For example, atom.properties.supercell.index == (2,1,0) means that atom is a copy of atom.properties.supercell.origin that was translated twice along the first lattice vector, once along the second vector, and not translated along the third vector.

Example usage:

>>> graphene = Molecule('graphene.xyz')
>>> print(graphene)
  Atoms:
    1         C      0.000000      0.000000      0.000000
    2         C      1.230000      0.710000      0.000000
  Lattice:
        2.4600000000     0.0000000000     0.0000000000
        1.2300000000     2.1304224933     0.0000000000

>>> graphene_supercell = graphene.supercell(2,2) # diagonal supercell expansion
>>> print(graphene_supercell)
  Atoms:
    1         C      0.000000      0.000000      0.000000
    2         C      1.230000      0.710000      0.000000
    3         C      1.230000      2.130422      0.000000
    4         C      2.460000      2.840422      0.000000
    5         C      2.460000      0.000000      0.000000
    6         C      3.690000      0.710000      0.000000
    7         C      3.690000      2.130422      0.000000
    8         C      4.920000      2.840422      0.000000
  Lattice:
        4.9200000000     0.0000000000     0.0000000000
        2.4600000000     4.2608449866     0.0000000000

>>> diamond = Molecule('diamond.xyz')
>>> print(diamond)
  Atoms:
    1         C     -0.446100     -0.446200     -0.446300
    2         C      0.446400      0.446500      0.446600
  Lattice:
        0.0000000000     1.7850000000     1.7850000000
        1.7850000000     0.0000000000     1.7850000000
        1.7850000000     1.7850000000     0.0000000000

>>> diamond_supercell = diamond.supercell([[-1,1,1],[1,-1,1],[1,1,-1]])
>>> print(diamond_supercell)
  Atoms:
    1         C     -0.446100     -0.446200     -0.446300
    2         C      0.446400      0.446500      0.446600
    3         C      1.338900      1.338800     -0.446300
    4         C      2.231400      2.231500      0.446600
    5         C      1.338900     -0.446200      1.338700
    6         C      2.231400      0.446500      2.231600
    7         C     -0.446100      1.338800      1.338700
    8         C      0.446400      2.231500      2.231600
  Lattice:
        3.5700000000     0.0000000000     0.0000000000
        0.0000000000     3.5700000000     0.0000000000
        0.0000000000     0.0000000000     3.5700000000

unit_cell_volume(unit='angstrom')[source]¶

Return the volume of the unit cell of a 3D system.

unit is the unit of length, the cube of which will be used as the unit of volume.

cell_lengths(unit='angstrom')[source]¶

Return the lengths of the lattice vector. Returns a list with the same length as self.lattice

cell_angles(unit='degree')[source]¶

Return the angles between lattice vectors.

unitstr

output unit

For 2D systems, returns a list [gamma]

For 3D systems, returns a list [alpha, beta, gamma]

set_integer_bonds(action='warn', tolerance=0.0001)[source]¶

Convert non-integer bond orders into integers.

For example, bond orders of aromatic systems are no longer set to the non-integer value of 1.5, instead adopting bond orders of 1 and 2.

The implemented function walks a set of graphs constructed from all non-integer bonds, converting the orders of aforementioned bonds to integers by alternating calls to math.ceil() and math.floor(). The implication herein is that both \(i\) and \(i+1\) are considered valid (integer) values for any bond order within the \((i, i+1)\) interval. Floats which can be represented exactly as an integer, e.g. \(1.0\), are herein treated as integers.

Can be used for sanitizing any Molecules passed to the rdkit module, as its functions are generally unable to handle Molecules with non-integer bond orders.

By default this function will issue a warning if the total (summed) bond orders before and after are not equal to each other within a given tolerance. Accepted values are for action are "ignore", "warn" and "raise", which respectively ignore such cases, issue a warning or raise a MoleculeError.

>>> from scm.plams import Molecule

>>> benzene = Molecule(...)
>>> print(benzene)
  Atoms:
    1         C      1.193860     -0.689276      0.000000
    2         C      1.193860      0.689276      0.000000
    3         C      0.000000      1.378551      0.000000
    4         C     -1.193860      0.689276      0.000000
    5         C     -1.193860     -0.689276      0.000000
    6         C     -0.000000     -1.378551      0.000000
    7         H      2.132911     -1.231437     -0.000000
    8         H      2.132911      1.231437     -0.000000
    9         H      0.000000      2.462874     -0.000000
   10         H     -2.132911      1.231437     -0.000000
   11         H     -2.132911     -1.231437     -0.000000
   12         H     -0.000000     -2.462874     -0.000000
  Bonds:
   (3)--1.5--(4)
   (5)--1.5--(6)
   (1)--1.5--(6)
   (2)--1.5--(3)
   (4)--1.5--(5)
   (1)--1.5--(2)
   (3)--1.0--(9)
   (6)--1.0--(12)
   (5)--1.0--(11)
   (4)--1.0--(10)
   (2)--1.0--(8)
   (1)--1.0--(7)

>>> benzene.set_integer_bonds()
>>> print(benzene)
  Atoms:
    1         C      1.193860     -0.689276      0.000000
    2         C      1.193860      0.689276      0.000000
    3         C      0.000000      1.378551      0.000000
    4         C     -1.193860      0.689276      0.000000
    5         C     -1.193860     -0.689276      0.000000
    6         C     -0.000000     -1.378551      0.000000
    7         H      2.132911     -1.231437     -0.000000
    8         H      2.132911      1.231437     -0.000000
    9         H      0.000000      2.462874     -0.000000
   10         H     -2.132911      1.231437     -0.000000
   11         H     -2.132911     -1.231437     -0.000000
   12         H     -0.000000     -2.462874     -0.000000
  Bonds:
   (3)--1.0--(4)
   (5)--1.0--(6)
   (1)--2.0--(6)
   (2)--2.0--(3)
   (4)--2.0--(5)
   (1)--1.0--(2)
   (3)--1.0--(9)
   (6)--1.0--(12)
   (5)--1.0--(11)
   (4)--1.0--(10)
   (2)--1.0--(8)
   (1)--1.0--(7)

index(value, start=1, stop=None)[source]¶

Return the first index of the specified Atom or Bond.

Providing an Atom will return its 1-based index, while a Bond returns a 2-tuple with the 1-based indices of its atoms.

Raises a MoleculeError if the provided is not an Atom/Bond or if the Atom/bond is not part of the molecule.

>>> from scm.plams import Molecule, Bond, Atom

>>> mol = Molecule(...)
>>> atom: Atom = Molecule[1]
>>> bond: Bond = Molecule[1, 2]

>>> print(mol.index(atom))
1

>>> print(mol.index(bond))
(1, 2)

round_coords(decimals=0, inplace=True)[source]¶

Round the Cartesian coordinates of this instance to decimals.

By default, with inplace=True, the coordinates of this instance are updated inplace. If inplace=False then a new copy of this Molecule is returned with its coordinates rounded.

>>> from scm.plams import Molecule

>>> mol = Molecule(...)
  Atoms:
    1         H      1.234567      0.000000      0.000000
    2         H      0.000000      0.000000      0.000000

>>> mol_rounded = round_coords(mol)
>>> print(mol_rounded)
  Atoms:
    1         H      1.000000      0.000000      0.000000
    2         H      0.000000      0.000000      0.000000

>>> mol.round_coords(decimals=3)
>>> print(mol)
  Atoms:
    1         H      1.234000      0.000000      0.000000
    2         H      0.000000      0.000000      0.000000

get_connection_table()[source]¶

Get a connection table with atom indices (starting at 0)

get_molecule_indices()[source]¶

Use the bond information to identify submolecules

Returns a list of lists of indices (e.g. for two methane molecules: [[0,1,2,3,4],[5,6,7,8,9]])

get_fragment(indices)[source]¶

Return a submolecule from self

get_complete_molecules_within_threshold(atom_indices, threshold)[source]¶

Returns a new molecule containing complete submolecules for any molecules that are closer than threshold to any of the atoms in atom_indices.

Note: This only works for non-periodic systems.

atom_indices: list of int

One-based indices of the atoms

thresholdfloat

Distance threshold for whether to include molecules

locate_rings()[source]¶

Find the rings in the structure

locate_rings_acm(all_rings=True)[source]¶

Use the ACM algorithm to find rings

• all_rings – If all_rings is set to False, this algorithm reverts to SSSR

Note: This is actually Paton’s algorithm

to find the fundamental cycles in a graph The basis of fundamental cycles is found if all_rings is set to False Otherwise, for each edge not in the spanning tree, all cycles of the same length are added. So there may be more than one cycle for each of these edges. That is the same result as locate_rings() gives, but faster. The RDKit SSSR algorithm (which in that case stands for small set of smallest rings) returns more rings than regular SSSR, but less than this algorithm with allrings=True. I am not sure what RDKit does exactly, and I cannot see the pattern in the results. It looks inconsistent (compare results for ‘CC1C2=CCC3=CC=CC=CC=CCOCC4CCC(C2=C3)=C2C=1CCCC24’ and ‘CC1C2=CCC3=CC=CC=CC=CC4CCCCCC5CCC6C(=C(CCC6CO4)C2=C3)C=15’).

order_ring(ring_indices)[source]¶

Order the ring indices so that they are sequential along the ring

locate_rings_networkx(find_smallest=False)[source]¶

Obtain a list of ring indices using networkx (same as locate_rings, but much faster)

• find_smallest – Advised if the rings themselves will be used. Does not affect the number of rings.

Note: The SSSR (smallest set of smallest rings) algorithm.

In contrast, RDKit uses a ‘small set of smallest rings’ algorithm. The SSSR is more reliable than the other two locate_rings methods, as well as the RDKit alternative. It may only assign 5 rings to cubane, but it is generally more consistent.

shortest_path_dijkstra(source, target, conect=None)[source]¶

Find the shortest paths (can be more than 1) between a source atom and a target atom in a connection table

• source – Index of the source atom

• target – Index of the target atom

translate(vector, unit='angstrom')[source]¶

Move the molecule in space by vector, expressed in unit.

vector should be an iterable container of length 3 (usually tuple, list or numpy array). unit describes unit of values stored in vector.

rotate_lattice(matrix)[source]¶

Rotate only lattice vectors of the molecule with given rotation matrix.

matrix should be a container with 9 numerical values. It can be a list (tuple, numpy array etc.) listing matrix elements row-wise, either flat ([1,2,3,4,5,6,7,8,9]) or in two-level fashion ([[1,2,3],[4,5,6],[7,8,9]]).

Note

This method does not check if matrix is a proper rotation matrix.

rotate(matrix, lattice=False)[source]¶

Rotate the molecule with given rotation matrix. If lattice is True, rotate lattice vectors too.

matrix should be a container with 9 numerical values. It can be a list (tuple, numpy array etc.) listing matrix elements row-wise, either flat ([1,2,3,4,5,6,7,8,9]) or in two-level fashion ([[1,2,3],[4,5,6],[7,8,9]]).

Note

This method does not check if matrix is a proper rotation matrix.

align_lattice(convention='AMS', zero=1e-10)[source]¶

Rotate the molecule in such a way that lattice vectors are aligned with the coordinate system.

This method is meant to be used with periodic systems only. Using it on a Molecule instance with an empty lattice attribute has no effect.

Possible values of the convention argument are:

• AMS (default) – for 1D systems the lattice vector aligned with X axis. For 2D systems both lattice vectors aligned with XY plane. No constraints for 3D systems

• reax (convention used by ReaxFF) – second lattice vector (if present) aligned with YZ plane. Third vector (if present) aligned with Z axis.

zero argument can be used to specify the numerical tolerance for zero (used to determine if some vector is already aligned with a particular axis or plane).

The returned boolean value indicates if any rotation happened.

rotate_bond(bond, moving_atom, angle, unit='radian')[source]¶

Rotate part of this molecule containing moving_atom along axis defined by bond by an angle expressed in unit.

bond should be chosen in such a way, that it divides the molecule into two parts (using a bond that forms a ring results in a MoleculeError). moving_atom has to belong to bond and is used to pick which part of the molecule is rotated. A positive angle denotes counterclockwise rotation (when looking along the bond, from the stationary part of the molecule).

resize_bond(bond, moving_atom, length, unit='angstrom')[source]¶

Change the length of bond to length expressed in unit by moving part of the molecule containing moving_atom

bond should be chosen in such a way, that it divides the molecule into two parts (using a bond that forms a ring results in a MoleculeError). moving_atom has to belong to bond and is used to pick which part of the molecule is moved.

closest_atom(point, unit='angstrom')[source]¶

Return the atom of the molecule that is the closest one to some point in space.

point should be an iterable container of length 3 (for example: tuple, Atom, list, numpy array). unit describes unit of values stored in point.

distance_to_point(point, unit='angstrom', result_unit='angstrom')[source]¶

Calculate the distance between the molecule and some point in space (distance between point and closest_atom()).

point should be an iterable container of length 3 (for example: tuple, Atom, list, numpy array). unit describes unit of values stored in point. Returned value is expressed in result_unit.

distance_to_mol(other, result_unit='angstrom', return_atoms=False)[source]¶

Calculate the distance between the molecule and some other molecule.

The distance is measured as the smallest distance between any atom of this molecule and any atom of other molecule. Returned distance is expressed in result_unit.

If return_atoms is False, only a single number is returned. If return_atoms is True, the method returns a tuple (distance, atom1, atom2) where atom1 and atom2 are atoms fulfilling the minimal distance, with atom1 belonging to this molecule and atom2 to other.

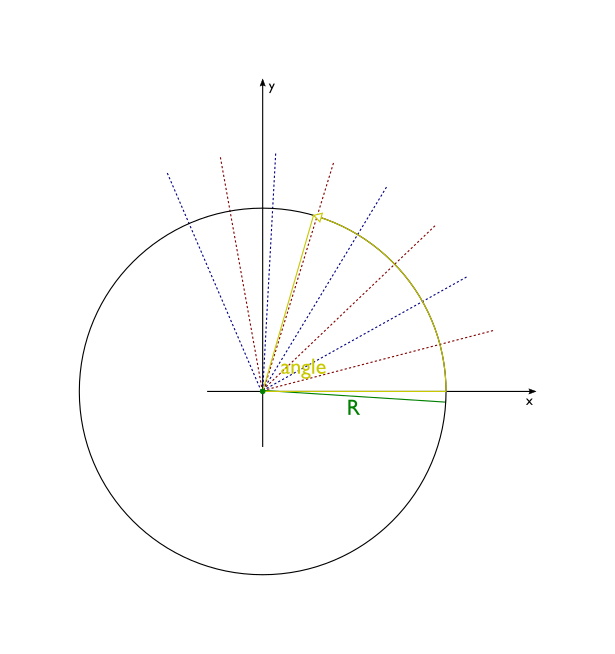
wrap(self, length, angle=2 * pi, length_unit='angstrom', angle_unit='radian')[source]¶

Transform the molecule wrapping its x-axis around z-axis. This method is useful for building nanotubes or molecular wedding rings.

Atomic coordinates are transformed in the following way:

• z coordinates remain untouched

• x axis gets wrapped around the circle centered in the origin of new coordinate system. Each segment of x axis of length length ends up as an arc of a circle subtended by an angle angle. The radius of this circle is R = length/angle.

• part of the plane between the x axis and the line y=R is transformed into the interior of the circle, with line y=R being squashed into a single point - the center of the circle.

• part of the plane above line y=R is dropped

• part of the plane below x axis is transformed into outside of the circle

• transformation is done in such a way that distances along y axis are preserved

Before:

After:

get_center_of_mass(unit='angstrom')[source]¶

Return the center of mass of the molecule (as a tuple). Returned coordinates are expressed in unit.

get_masses(unit='amu')[source]¶

Return list of masses, by default in atomic mass units.

get_mass(unit='amu')[source]¶

Return the mass of the molecule, by default in atomic mass units.

get_density()[source]¶

Return the density in kg/m^3

set_density(density)[source]¶

Applies a uniform strain so that the density becomes density kg/m^3

get_formula(as_dict=False)[source]¶

Calculate the molecular formula of the molecule according to the Hill system.

Here molecular formula is a dictionary with keys being atomic symbols. The value for each key is the number of atoms of that type. If as_dict is True, that dictionary is returned. Otherwise, it is converted into a string:

>>> mol = Molecule('Ubiquitin.xyz')
>>> print(m.get_formula(True))
{'N': 105, 'C': 378, 'O': 118, 'S': 1, 'H': 629}
>>> print(m.get_formula(False))
C378H629N105O118S1

get_inertia_matrix(length_unit='angstrom', mass_unit='amu')[source]¶

Get the moments of inertia matrix.

Parameters:

• length_unit (str, optional) – unit for distance. Defaults to ‘angstrom’.

• mass_unit (str, optional) – unit for mass. Defaults to ‘amu’.

Returns:

3x3 matrix with the inertia matrix

Return type:

np.ndarray

get_moments_of_inertia(eigen_vectors=False, length_unit='angstrom', mass_unit='amu')[source]¶

Get the moments of inertia along the principal axes (in amu*angstrom**2 by default). They are computed from the eigenvalues of the symmetric inertial tensor. Optionally the eigenvectors can be returned.

Parameters:

• eigen_vectors (bool, optional) – return also the eigen_vectors. Defaults to False.

• length_unit (str, optional) – unit for distance. Defaults to ‘angstrom’.

• mass_unit (str, optional) – unit for mass. Defaults to ‘amu’.

Returns:

moments of inertia [(3,)] and optionally the eigenvectors

Return type:

np.ndarray or Tuple(np.ndarray, np.ndarray)

get_gyration_radius(unit='angstrom')[source]¶

Return the gyration radius of the molecule by default in angstrom. It gives information about the overall dimensions of the rotating molecule around its center of mass.

Parameters:

unit (str, optional) – unit for distance. Defaults to ‘angstrom’.

Returns:

gyration radius of the molecule in unit.

Return type:

float

apply_strain(strain, voigt_form=False)[source]¶

Apply a strain deformation to a periodic system (i.e. with a non-empty lattice attribute). The atoms in the unit cell will be strained accordingly, keeping the fractional atomic coordinates constant.

If voigt_form=False, strain should be a container with n*n numerical values, where n is the number of lattice vectors. It can be a list (tuple, numpy array etc.) listing matrix elements row-wise, either flat (e.g. [e_xx, e_xy, e_xz, e_yx, e_yy, e_yz, e_zx, e_zy, e_zz]) or in two-level fashion (e.g. [[e_xx, e_xy, e_xz],[e_yx, e_yy, e_yz],[e_zx, e_zy, e_zz]]). If voigt_form=True, strain should be passed in Voigt form (for 3D periodic systems: [e_xx, e_yy, e_zz, gamma_yz, gamma_xz, gamma_xy]; for 2D periodic systems: [e_xx, e_yy, gamma_xy]; for 1D periodic systems: [e_xx] with e_xy = gamma_xy/2,…). Example usage:

>>> graphene = Molecule('graphene.xyz')
>>> print(graphene)
  Atoms:
    1         C      0.000000      0.000000      0.000000
    2         C      1.230000      0.710141      0.000000
  Lattice:
        2.4600000000     0.0000000000     0.0000000000
        1.2300000000     2.1304224900     0.0000000000
>>> graphene.apply_strain([0.1,0.2,0.0], voigt_form=True)])
  Atoms:
    1         C      0.000000      0.000000      0.000000
    2         C      1.353000      0.852169      0.000000
  Lattice:
        2.7060000000     0.0000000000     0.0000000000
        1.3530000000     2.5565069880     0.0000000000

map_to_central_cell(around_origin=True)[source]¶

Maps all atoms to the original cell. If around_origin=True the atoms will be mapped to the cell with fractional coordinates [-0.5,0.5], otherwise to the the cell in which all fractional coordinates are in the [0:1] interval.

perturb_atoms(max_displacement=0.01, unit='angstrom', atoms=None)[source]¶

Randomly perturb the coordinates of the atoms in the molecule.

Each Cartesian coordinate is displaced by a random value picked out of a uniform distribution in the interval [-max_displacement, +max_displacement] (converted to requested unit).

By default, all atoms are perturbed. It is also possible to perturb only part of the molecule, indicated by atoms argument. It should be a list of atoms belonging to the molecule.

perturb_lattice(max_displacement=0.01, unit='angstrom', ams_convention=True)[source]¶

Randomly perturb the lattice vectors.

The Cartesian components of the lattice vectors are changed by a random value picked out of a uniform distribution in the interval [-max_displacement, +max_displacement] (converted to requested unit).

If ams_convention=True then for 1D-periodic systems only the x-component of the lattice vector is perturbed, and for 2D-periodic systems only the xy-components of the lattice vectors are perturbed.

substitute(connector, ligand, ligand_connector, bond_length=None, steps=12, cost_func_mol=None, cost_func_array=None)[source]¶

Substitute a part of this molecule with ligand.

connector should be a pair of atoms that belong to this molecule and form a bond. The first atom of connector is the atom to which the ligand will be connected. The second atom of connector is removed from the molecule, together with all “further” atoms connected to it (that allows, for example, to substitute the whole functional group with another). Using connector that is a part or a ring triggers an exception.

ligand_connector is a connector analogue, but for ligand. IT describes the bond in the ligand that will be connected with the bond in this molecule described by connector.

If this molecule or ligand don’t have any bonds, guess_bonds() is used.

After removing all unneeded atoms, the ligand is translated to a new position, rotated, and connected by bond with the core molecule. The new Bond is added between the first atom of connector and the first atom of ligand_connector. The length of that bond can be adjusted with bond_length argument, otherwise the default is the sum of atomic radii taken from PeriodicTable.

Then the ligand is rotated along newly created bond to find the optimal position. The full 360 degrees angle is divided into steps equidistant rotations and each such rotation is evaluated using a cost function. The orientation with the minimal cost is chosen.

The default cost function is:

\[\sum_{i \in mol, j\in lig} e^{-R_{ij}}\]

A different cost function can be also supplied by the user, using one of the two remaining arguments: cost_func_mol or cost_func_array. cost_func_mol should be a function that takes two Molecule instances: this molecule (after removing unneeded atoms) and ligand in a particular orientation (also without unneeded atoms) and returns a single number (the lower the number, the better the fit). cost_func_array is analogous, but instead of Molecule instances it takes two numpy arrays (with dimensions: number of atoms x 3) with coordinates of this molecule and the ligand. If both are supplied, cost_func_mol takes precedence over cost_func_array.

map_atoms_to_bonds()[source]¶

Corrects for lattice displacements along bonds

Uses a breadth-first search to map the atoms bond by bond (wrap)

__repr__()[source]¶

Return repr(self).

__len__()[source]¶

The length of the molecule is the number of atoms.

__str__()[source]¶

Return str(self).

str(decimal=6)[source]¶

Return a string representation of the molecule.

Information about atoms is printed in xyz format fashion – each atom in a separate, enumerated line. Then, if the molecule contains any bonds, they are printed. Each bond is printed in a separate line, with information about both atoms and bond order. Example:

Atoms:
  1         N       0.00000       0.00000       0.38321
  2         H       0.94218       0.00000      -0.01737
  3         H      -0.47109       0.81595      -0.01737
  4         H      -0.47109      -0.81595      -0.01737
Bonds:
  (1)----1----(2)
  (1)----1----(3)
  (1)----1----(4)

__iter__()[source]¶

Iterate over atoms.

__getitem__(key)[source]¶

The bracket notation can be used to access atoms or bonds directly.

If key is a single int (mymol[i]), return i-th atom of the molecule. If key is a pair of ints (mymol[(i,j)]), return the bond between i-th and j-th atom (None if such a bond does not exist). Negative integers can be used to access atoms enumerated in the reversed order.

This notation is read only: things like mymol[3] = Atom(...) are forbidden.

Numbering of atoms within a molecule starts with 1.

__add__(other)[source]¶

Create a new molecule that is a sum of this molecule and some other molecule:

newmol = mol1 + mol2

The new molecule has atoms, bonds and all other elements distinct from both components. The properties of newmol are a copy of the properties of mol1 soft_updated with the properties of mol2.

__iadd__(other)[source]¶

Copy other molecule and add the copy to this one.

__round__(ndigits=None)[source]¶

Magic method for rounding this instance’s Cartesian coordinates; called by the builtin round() function.

__getstate__()[source]¶

Returns the object which is to-be pickled by, e.g., pickle.dump(). As Molecule instances are heavily nested objects, pickling them can raise a RecursionError. This issue is herein avoided relying on the Molecule.as_dict() method. See Pickling Class Instances for more details.

__setstate__(state)[source]¶

Counterpart of Molecule.__getstate__(); used for unpickling molecules.

as_dict()[source]¶

Store all information about the molecule in a dictionary.

The returned dictionary is, in principle, identical to self.__dict__ of the current instance, apart from the fact that all Atom and Bond instances in atoms and bonds lists are replaced with dictionaries storing corresponding information.

This method is a counterpart of from_dict().

classmethod from_dict(dictionary)[source]¶

Generate a new Molecule instance based on the information stored in a dictionary.

This method is a counterpart of as_dict().

classmethod from_elements(elements)[source]¶

Generate a new Molecule instance based on a list of elements.

By default it sets all coordinates to zero

property as_array¶

mol.as_array() or as a context manager with mol.as_array. Take care of when to add the parentheses.

Return cartesian coordinates of this molecule’s atoms as a numpy array.

atom_subset argument can be used to specify only a subset of atoms, it should be an iterable container with atoms belonging to this molecule.

Returned value is a n*3 numpy array where n is the number of atoms in the whole molecule, or in atom_subset, if used.

Alternatively, this property can be used in conjunction with the with statement, which automatically calls Molecule.from_array() upon exiting the context manager. Note that the molecules’ coordinates will be updated based on the array that was originally returned, so creating and operating on a copy thereof will not affect the original molecule.

>>> from scm.plams import Molecule
>>> mol = Molecule(...)
>>> with mol.as_array as xyz_array:
>>>     xyz_array += 5.0
>>>     xyz_array[0] = [0, 0, 0]
# Or equivalently
>>> xyz_array = mol.as_array()
>>> xyz_array += 5.0
>>> xyz_array[0] = [0, 0, 0]
>>> mol.from_array(xyz_array)

Type:

Property that can either be called directly as a method

from_array(xyz_array, atom_subset=None)[source]¶

Update the cartesian coordinates of this Molecule, containing n atoms, with coordinates provided by a (≤n)*3 numpy array xyz_array.

atom_subset argument can be used to specify only a subset of atoms, it should be an iterable container with atoms belonging to this molecule. It should have the same length as the first dimension of xyz_array.

__array__(dtype=None)[source]¶

A magic method for constructing numpy arrays.

This method ensures that passing a Molecule instance to numpy.array produces an array of Cartesian coordinates (see Molecule.as_array()). The array data type can, optionally, be specified in dtype.

readxyz(f, geometry=1, **other)[source]¶

XYZ Reader:

The xyz format allows to store more than one geometry of a particular molecule within a single file. In such cases the geometry argument can be used to indicate which (in order of appearance in the file) geometry to import. Default is the first one (geometry = 1).

writexyz(f, space=16, decimal=8)[source]¶

f: file

An open file handle.

See also the write method: molecule.write(“my_molecule.xyz”)

example:

with open(path_to_xyz_molecule_file, 'w') as f:
    molecule.writexyz(f)

readpdb(f, geometry=1, **other)[source]¶

PDB Reader:

The pdb format allows to store more than one geometry of a particular molecule within a single file. In such cases the geometry argument can be used to indicate which (in order of appearance in the file) geometry to import. The default is the first one (geometry = 1).

writepdb(f, **other)[source]¶

Write the molecule in PDB format

hydrogen_to_deuterium()[source]¶

Modifies the current molecule so that all hydrogen atoms get mass 2.014 by modifying the atom.properties.mass

static _mol_from_rkf_section(sectiondict)[source]¶

Return a Molecule instance constructed from the contents of the whole .rkf file section, supplied as a dictionary returned by KFFile.read_section.

forcefield_params_from_rkf(filename)[source]¶

Read all force field data from a forcefield.rkf file into self

• filename – Name of the RKF file that contains ForceField data

readin(f, **other)[source]¶

Read a file containing a System block used in AMS driver input files.

writein(f, **other)[source]¶

Write the Molecule instance to a file as a System block from the AMS driver input files.

read(filename, inputformat=None, **other)[source]¶

Read molecular coordinates from a file.

filename should be a string with a path to a file. If inputformat is not None, it should be one of supported formats or engines (keys occurring in the class attribute _readformat). Otherwise, the format is deduced from the file extension. For files without an extension the xyz format is used.

All other options are passed to the chosen format reader.

write(filename, outputformat=None, mode='w', **other)[source]¶

Write molecular coordinates to a file.

filename should be a string with a path to a file. If outputformat is not None, it should be one of supported formats or engines (keys occurring in the class attribute _writeformat). Otherwise, the format is deduced from the file extension. For files without an extension the xyz format is used.

mode can be either ‘w’ (overwrites the file if the file exists) or ‘a’ (appends to the file if the file exists).

All other options are passed to the chosen format writer.

add_hatoms()[source]¶

Adds missing hydrogen atoms to the current molecule. Returns a new Molecule instance.

Example:

>>> o = Molecule()
>>> o.add_atom(Atom(atnum=8))
>>> print(o)
  Atoms:
    1         O      0.000000       0.000000       0.000000
>>> h2o = o.add_hatoms()
>>> print(h2o)
  Atoms:
    1         O      0.000000       0.000000       0.000000
    2         H     -0.109259       0.893161       0.334553
    3         H      0.327778       0.033891      -0.901672

static rmsd(mol1, mol2, ignore_hydrogen=False, return_rotmat=False, check=True)[source]¶

Uses the Kabsch algorithm to align and calculate the root-mean-square deviation of two systems’ atomic positions.

Assumes all elements and their order is the same in both systems, will check this if check == True.

Returns:

rmsdfloat

Root-mean-square-deviation of atomic coordinates

rotmatndarray

If return_rotmat is True, will additionally return the rotation matrix that aligns mol2 onto mol1.

align2mol(molecule_ref, ignore_hydrogen=False, watch=False)[source]¶

align the molecule to a reference molecule, they should be same molecule type and same order of atoms it is an wrapper of the rmsd methods if watch = True show the molecules (before and after) in a Jupyter notebook

assign_chirality()¶

Assigns stereo-info to PLAMS molecule by invoking RDKIT

find_permutation(other, level=1)¶

Reorder atoms in this molecule to match the order in some other molecule. The reordering is applied only if the perfect match is found. Returned value is the applied permutation (as a list of integers) or None, if no reordering was performed.

get_chirality()¶

Returns the chirality of the atoms

label(level=1, keep_labels=False, flags=None)¶

Compute the label of this molecule using chosen level of detail.

Possible levels are:

• 0: does not perform any atom labeling, returns empirical formula (see get_formula())

• 1: only direct connectivity is considered, without bond orders (in other words, treats all the bonds as single bonds)

• 2: use connectivity and bond orders

• 3: use connectivity, bond orders and some spatial information to distinguish R/S and E/Z isomers

• 4: use all above, plus more spatial information to distinguish different rotamers and different types of coordination complexes

If you need more precise control of what is taken into account while computing the label (or adjust the tolerance for geometrical operations) you can use the flags argument. It should be a dictionary of parameters recognized by label_atoms(). Each of two letter boolean flags has to be present in flags. If you use flags, level is ignored.

The level argument can also be a tuple of integers. In that case the labeling algorithm is run multiple times and the returned value is a tuple (with the same length as level) containing labels calculated with given levels of detail.

This function, by default, erases IDname attributes of all atoms at the end. You can change this behavior with keep_labels argument.

If the molecule does not contain bonds, guess_bonds() is used to determine them.

Note

This method is a new PLAMS feature and it’s still somewhat experimental. The exact details of the algorithm can, and probably will, change in future. You are more than welcome to provide any feedback or feature requests.

property numbers¶

Return an array of all atomic numbers in the Molecule. Can also be used to set all numbers at once.

readase(f, **other)¶

Read Molecule using ASE engine

The read function of the Molecule class passes a file descriptor into here, so in this case you must specify the format to be read by ASE:

mol = Molecule('file.cif', inputformat='ase', format='cif')

The ASE Atoms object then gets converted to a PLAMS Molecule and returned. All other options are passed to ASE.io.read(). See https://wiki.fysik.dtu.dk/ase/ase/io/io.html on how to use it.

Note

The nomenclature of PLAMS and ASE is incompatible for reading multiple geometries, make sure that you only read single geometries with ASE! Reading multiple geometries is not supported, each geometry needs to be read individually.

set_local_labels(niter=2, flags=None)¶

Set atomic labels (IDnames) that are unique for local structures of a molecule

• niter – The number of iterations in the atom labeling scheme

The idea of this method is that the number of iterations can be specified. If kept low (default niter), local structures over different molecules will have the same label.

writease(f, **other)¶

Write molecular coordinates using ASE engine.

The write function of the Molecule class passes a file descriptor into here, so in this case you must specify the format to be written by ASE. All other options are passed to ASE.io.write(). See https://wiki.fysik.dtu.dk/ase/ase/io/io.html on how to use it.

These two write the same content to the respective files:

molecule.write('filename.anyextension', outputformat='ase', format='gen')
molecule.writease('filename.anyextension', format='gen')

property symbols¶

Return an array of all atomic symbols in the Molecule. Can also be used to set all symbols at once.

_get_bond_id(at1, at2, id_type)[source]¶

at1: Atom in this molecule at2: Atom in this molecule id_type: str, ‘IDname’ or ‘symbol’ This function is called by get_unique_bonds()

Returns: a 2-tuple, the key and a bool. The bool is True if the order was reversed.

get_unique_bonds(ignore_dict=None, id_type='symbol', index_start=1)[source]¶

Returns a dictionary of all unique bonds in this molecule, where the key is the identifier and the value is a 2-tuple containing the 1-based indices of the atoms making up the bond (or 0-based indices if index_start == 0).

ignore_dictdict

Bonds already existing in ignore_dict (as defined by the keys) will not be added to the returned dictionary

Example: if id_type == ‘symbol’ and ignore_dict has a key ‘C-C’, then no C-C bond will be added to the return dictionary.

id_type: str

‘symbol’: The atomic symbols become the keys, e.g. ‘C-H’ (alphabetically sorted)

‘IDname’: The IDname from molecule.set_local_labels() become the keys, e.g. ‘an4va8478432bfl471baf74-knrq78jhkhq78fak111nf’ (alphabetically sorted). Note: You must first call Molecule.set_local_labels()

index_startint

If 1, indices are 1-based. If 0, indices are 0-based.

get_unique_angles(ignore_dict=None, id_type='symbol', index_start=1)[source]¶

Returns a dictionary of all unique angles in this molecule, where the key is the identifier and the value is a 3-tuple containing the 1-based indices of the atoms making up the angle (or 0-based indices if index_start == 0). The central atom is the second atom.

ignore_dictdict

Angles already existing in ignore_dict (as defined by the keys) will not be added to the returned dictionary

Example: if id_type == ‘symbol’ and ignore_dict has a key ‘C-C-C’, then no C-C-C angle will be added to the return dictionary.

id_type: str

‘symbol’: The atomic symbols become the keys, e.g. ‘C-C-C’ (alphabetically sorted, the central atom in the middle)

‘IDname’: The IDname from molecule.set_local_labels() become the keys, e.g. ‘an4va8478432bfl471baf74-knrq78jhkhq78fak111nf-mf42918vslahf879bakfhk’ (alphabetically sorted, the central atom in middle). Note: You must first call Molecule.set_local_labels()

index_startint

If 1, indices are 1-based. If 0, indices are 0-based.