Example: Gold electrodes¶
In this example of green, the self-energies are calculated of gold electrodes, the material most often used in molecular electronics. In the example for the Benzenedithiol junction these self-energies will be used to calculate the DOS and transmission of a benzenedithiol junction. The geometry of the electrodes is shown in Fig. 1.
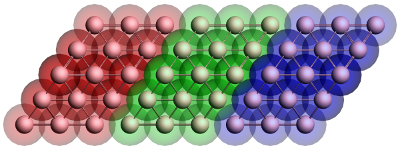
Figure 1: Geometry of the gold contact used in the calculation of the self-energy. The lead consists of two surface layers, left (red) and right (blue), and a bulk layer (green). Each principal layer in turn consists of three atomic layers. This should be sufficient to ensure that the Hamiltonian of the central (green) layer is a bulk Hamiltonian.
Each principal layer contains 3x3x3=27 gold atoms. For the calculation of the self-energies three principal layers are needed, and therefore 81 gold atoms in total. To keep the runtimes manageable it is therefore important to choose the basis set as small as possible. For transport calculations, a DZ basis with a large frozen core is generally sufficient. Unfortunately, even with the largest frozen core (Au.4f), the basis set for Au still contains 19 electrons. A significant speedup can be obtained by limiting this to 11 electrons (only the outer d and s shells). Be advised that even with this reduction the total runtime of calculation can be long.
To facilitate the calculation of the electrodes, first a gold atom fragment will be calculated with the smallest possible basis. The sample directory contains the required Au.5p and Au.5p.dirac files. Note that for gold relativistic effects are important. Therefore RELATIVISTIC Scalar ZORA will be used throughout this example.
$ADFBIN/dirac < Au.5p.dirac
mv TAPE12 t12.rel
$ADFBIN/adf -n1 << eor
CREATE Au file=Au.5p
RELATIVISTIC Scalar ZORA
COREPOTENTIALS t12.rel
XC
LDA SCF VWN
END
eor
mv TAPE21 t21.Au
$ADFBIN/adf << eor
TITLE Gold atom
ATOMS
Au 0.000000 0.000000 0.000000
END
RELATIVISTIC Scalar ZORA
FRAGMENTS
Au t21.Au
END
XC
LDA SCF VWN
END
eor
mv TAPE21 Au.t21
A principal layer of gold consists of three atomic layers, which should be sufficient due to the small screening length. An atomic layer contains 3x3=9 atoms in a (111) FCC configuration. This allows one to use the top-, bride-, and hollow-site binding configurations for a molecule. For the following calculations it is necessary to first construct a fragment of a principal layer.
$ADFBIN/adf << eor
TITLE Principal layer
ATOMS
Au -2.355588 -6.662612 0.000000
Au -2.355589 -4.164133 -1.442498
Au -2.355589 -4.164133 1.442498
Au -2.355589 -1.665653 -2.884996
Au -2.355589 -1.665653 0.000000
Au -2.355589 -1.665653 2.884996
Au -2.355589 0.832826 -1.442498
Au -2.355589 0.832826 1.442498
Au -2.355589 3.331306 0.000000
Au 0.000000 -4.996959 0.000000
Au 0.000000 -2.498480 -1.442498
Au 0.000000 -2.498480 1.442498
Au 0.000000 0.000000 -2.884996
Au 0.000000 0.000000 0.000000
Au 0.000000 0.000000 2.884996
Au 0.000000 2.498480 -1.442498
Au 0.000000 2.498480 1.442498
Au 0.000000 4.996959 0.000000
Au 2.355589 -3.331306 0.000000
Au 2.355589 -0.832826 -1.442498
Au 2.355589 -0.832826 1.442498
Au 2.355589 1.665653 -2.884996
Au 2.355589 1.665653 0.000000
Au 2.355589 1.665653 2.884996
Au 2.355589 4.164133 -1.442498
Au 2.355589 4.164133 1.442498
Au 2.355588 6.662612 0.000000
END
SYMMETRY NOSYM
RELATIVISTIC Scalar ZORA
FRAGMENTS
Au Au.t21
END
XC
LDA SCF VWN
END
eor
mv TAPE21 layer.t21
Three principal layers are stacked together to calculate the self-energies (see Fig. 1). The names of the fragments are significant, since one needs to refer to them by name in the calculation of the self-energies.
$ADFBIN/adf << eor
TITLE Bulk gold
ATOMS
Au -9.422355 -11.659571 0.000000 f=left
Au -9.422356 -9.161092 -1.442498 f=left
Au -9.422356 -9.161092 1.442498 f=left
Au -9.422356 -6.662612 -2.884996 f=left
Au -9.422356 -6.662612 0.000000 f=left
Au -9.422356 -6.662612 2.884996 f=left
Au -9.422356 -4.164133 -1.442498 f=left
Au -9.422356 -4.164133 1.442498 f=left
Au -9.422356 -1.665653 0.000000 f=left
Au -7.066767 -9.993918 0.000000 f=left
Au -7.066767 -7.495439 -1.442498 f=left
Au -7.066767 -7.495439 1.442498 f=left
Au -7.066767 -4.996959 -2.884996 f=left
Au -7.066767 -4.996959 0.000000 f=left
Au -7.066767 -4.996959 2.884996 f=left
Au -7.066767 -2.498479 -1.442498 f=left
Au -7.066767 -2.498479 1.442498 f=left
Au -7.066767 0.000000 0.000000 f=left
Au -4.711178 -8.328265 0.000000 f=left
Au -4.711178 -5.829785 -1.442498 f=left
Au -4.711178 -5.829785 1.442498 f=left
Au -4.711178 -3.331306 -2.884996 f=left
Au -4.711178 -3.331306 0.000000 f=left
Au -4.711178 -3.331306 2.884996 f=left
Au -4.711178 -0.832826 -1.442498 f=left
Au -4.711178 -0.832826 1.442498 f=left
Au -4.711179 1.665653 0.000000 f=left
Au -2.355588 -6.662612 0.000000 f=center
Au -2.355589 -4.164133 -1.442498 f=center
Au -2.355589 -4.164133 1.442498 f=center
Au -2.355589 -1.665653 -2.884996 f=center
Au -2.355589 -1.665653 0.000000 f=center
Au -2.355589 -1.665653 2.884996 f=center
Au -2.355589 0.832826 -1.442498 f=center
Au -2.355589 0.832826 1.442498 f=center
Au -2.355589 3.331306 0.000000 f=center
Au 0.000000 -4.996959 0.000000 f=center
Au 0.000000 -2.498480 -1.442498 f=center
Au 0.000000 -2.498480 1.442498 f=center
Au 0.000000 0.000000 -2.884996 f=center
Au 0.000000 0.000000 0.000000 f=center
Au 0.000000 0.000000 2.884996 f=center
Au 0.000000 2.498480 -1.442498 f=center
Au 0.000000 2.498480 1.442498 f=center
Au 0.000000 4.996959 0.000000 f=center
Au 2.355589 -3.331306 0.000000 f=center
Au 2.355589 -0.832826 -1.442498 f=center
Au 2.355589 -0.832826 1.442498 f=center
Au 2.355589 1.665653 -2.884996 f=center
Au 2.355589 1.665653 0.000000 f=center
Au 2.355589 1.665653 2.884996 f=center
Au 2.355589 4.164133 -1.442498 f=center
Au 2.355589 4.164133 1.442498 f=center
Au 2.355588 6.662612 0.000000 f=center
Au 4.711179 -1.665653 0.000000 f=right
Au 4.711178 0.832826 -1.442498 f=right
Au 4.711178 0.832826 1.442498 f=right
Au 4.711178 3.331306 -2.884996 f=right
Au 4.711178 3.331306 0.000000 f=right
Au 4.711178 3.331306 2.884996 f=right
Au 4.711178 5.829785 -1.442498 f=right
Au 4.711178 5.829785 1.442498 f=right
Au 4.711178 8.328265 0.000000 f=right
Au 7.066767 0.000000 0.000000 f=right
Au 7.066767 2.498479 -1.442498 f=right
Au 7.066767 2.498479 1.442498 f=right
Au 7.066767 4.996959 -2.884996 f=right
Au 7.066767 4.996959 0.000000 f=right
Au 7.066767 4.996959 2.884996 f=right
Au 7.066767 7.495439 -1.442498 f=right
Au 7.066767 7.495439 1.442498 f=right
Au 7.066767 9.993918 0.000000 f=right
Au 9.422356 1.665653 0.000000 f=right
Au 9.422356 4.164133 -1.442498 f=right
Au 9.422356 4.164133 1.442498 f=right
Au 9.422356 6.662612 -2.884996 f=right
Au 9.422356 6.662612 0.000000 f=right
Au 9.422356 6.662612 2.884996 f=right
Au 9.422356 9.161092 -1.442498 f=right
Au 9.422356 9.161092 1.442498 f=right
Au 9.422355 11.659571 0.000000 f=right
END
SYMMETRY NOSYM
RELATIVISTIC Scalar ZORA
FRAGMENTS
left layer.t21
center layer.t21
right layer.t21
END
XC
LDA SCF VWN
END
eor
mv TAPE21 bulk.t21
Similar to the other examples, the self-energies of the left and right contacts is calculated for 1000 energy points between -0.5 and 0 Hartree. This results in two keyfiles of approximately 2.5 GB each. Since the self-energies are independent of whatever is placed between the contacts, they can be reused many times.
$ADFBIN/green << eor
SURFACE bulk.t21
FRAGMENTS center right
END
EPS -0.5 0 1000
ETA 1e-6
eor
mv SURFACE left.kf
$ADFBIN/green << eor
SURFACE bulk.t21
FRAGMENTS center left
END
EPS -0.5 0 1000
ETA 1e-6
eor
mv SURFACE right.kf
In order to interpret transmissions calculated with these self-energies, it is necessary to know the location of the Fermi energy. An estimate for the Fermi energy can be obtained from the bulk SCF calculation by taking the average of the HOMO and LUMO energies, which in this case equals -0.195 Hartree.
Usually the self-energies will be used to calculate the transmission of a molecular junction. However, it is instructive to use a principal layer of gold as the “molecule” and study the DOS and transmission of bulk gold.
$ADFBIN/green << eor
DOS bulk.t21
TRANS bulk.t21
EPS -0.5 0 1000
ETA 1e-6
LEFT left.kf
FRAGMENT left
END
RIGHT right.kf
FRAGMENT right
END
NOSAVE DOS_B, TRANS_B
eor
The results are shown in the following figure:
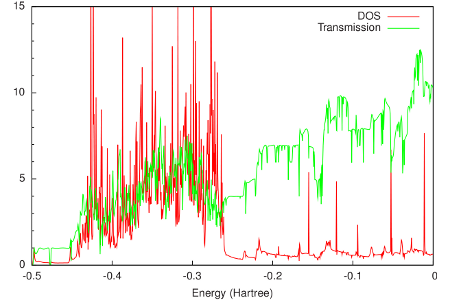
From this figure it can be seen that around the Fermi energy (-0.2 Hartree), both the DOS and the transmission of gold are relatively constant. This feature makes gold an attractive material for electrodes, since one can expect that the transmission of a molecular junction will be dominated by the molecular properties.