Lattice Optimization and Phonons

This tutorial will show you how to:

  • Perform a geometry optimization (including lattice vectors optimization) for a periodic system

  • Calculate and visualize the phonon dispersion curves

Set up the calculation

Let us begin by starting up the AMSinput GUI module:

1. Start AMSjobs
2. Click on SCM → New Input. This will open AMSinput
3. In AMSinput, select the DFTB panel: ADFPanel → DFTBPanel

Now we will import the silicon structure from our database:

1. Search for Si in the search box Search
2. Scroll down to the Crystals section and select Crystals → Si
/scm-uploads/doc.2023/Tutorials/_images/phonons_import_silicon.png

Phonons should be calculated for the optimal geometry. We therefore first need to perform a geometry optimization:

In the Main panel
1. Select Task → Geometry Optimization

By default, only the internal degrees of freedom are optimized in a geometry optimization (i.e. the atomic positions within the unit cell are optimized, but the lattice vectors are not optimized). In order to obtain a proper phonon spectrum, one needs to optimize the lattice vectors as well as the internal degrees of freedom. When optimizing the geometry for a phonon calculation, we generally recommend using tight convergence thresholds for both the nuclear and lattice degrees of freedom.

1. Click on Details → Geometry Optimization
2. Tick the Optimize Lattice check-box
3. Set the Convergence to Very Good
/scm-uploads/doc.2023/Tutorials/_images/phonons_geo_opt_details.png

Finally we also need to specify that we want to calculate phonons at the end of the optimization.

1. Switch to the Properties → Phonons and Elastic tensor panel
2. Tick the Phonons check-box

Optionally, you can tweak the settings of the phonon calculation in the panel Details → Phonons. Using a larger super cell in Details → Phonons will result in more accurate phonon curves, but will also significantly increase the computation time.

/scm-uploads/doc.2023/Tutorials/_images/phonons_enabled.png

We will now set a few options specific to DFTB.

1. Go to the Main panel
2. Select Model → SCC-DFTB
2. Select Parameter Directory → DFTB.org/hyb-0-2
3. Go to the Details → K-Space Integration panel
4. Set K-space grid type to Symmetric
/scm-uploads/doc.2023/Tutorials/_images/phonons_kspace.png

We explicitly ask for the symmetric k-space integration grid for our calculation of silicon, which is a highly symmetric system. For such a system the symmetric grid is more accurate and faster. However, unless your system is highly symmetric, we recommend using the default (regular) grid.

Run the calculation

We are now ready to run the calculation.

1. Click on File → Save and name it “silicon_phonons”
2. Click on File → Run

This will open AMSjobs and start the calculation. You can monitor the progress of your calculation by opening the log file:

In AMSjobs:
1. Right-click on your job and select Logfile to see the log file
2. Right-click on your job and select Movie to monitor the progress of the geometry optimization
3. Click on Graph → Lattice Vectors to monitor also the lattice optimization
3. Wait for the calculation to finish. It should only take a couple of steps.
/scm-uploads/doc.2023/Tutorials/_images/phonons_opt.png

As you can see the high symmetry of the system is maintained: All angles between the lattice vectors are 60 degrees and all vectors keep the same length. However, the entire crystal has expanded ever so slightly. (The strict nuclear gradients convergence threshold we set earlier actually did not matter, as all the nuclear gradients disappear due to the symmetry of the system. We were therefore essentially only optimizing the lattice degrees of freedom.)

Visualize the Phonons

Once the calculation is completed, you can visualize the phonon dispersion curves:

In AMSjobs, right-click on your job and select Band Structure

This will open the AMSbandstructure visualization program:

/scm-uploads/doc.2023/Tutorials/_images/phonons_dispersion.png

You can visualize the motion of the atoms for certain modes (marked by a blue dot in the dispersion curves):

Click on one of the “Modes” dots in the phonon dispersion curves
/scm-uploads/doc.2023/Tutorials/_images/phonons_modes.png

You can also visualize the electronic band structure and density of states computed by DFTB:

In the AMSbandstructure module, click on Options → Bandstructure
/scm-uploads/doc.2023/Tutorials/_images/phonons_band_structure.png

As expected, silicon has an indirect band gap.

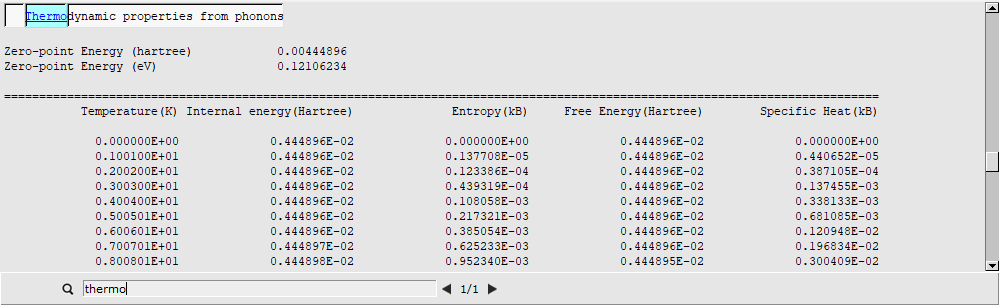
Thermodynamic properties derived from the phonon calculation are printed to the output file. To open the output file:

In AMSjobs, right-click on your job and select Output
In AMSoutput, search for “Thermo”
/scm-uploads/doc.2023/Tutorials/_images/phonons_out_thermo.png